链表中的快慢指针问题

链表应该是最常见的数据结构之一了，编程中经常使用到，由于其独特的特性，增删和修改都极其高效，但是随机读写却不如数组。在随机读写中，有一种巧妙的方式可以显著提升效率：快慢指针。

快慢指针

在遍历链表是使用步长一大一小的两个指针，因为步长不同，所以在从头遍历时，步长大的相对于步长小的看起来就跑的更“快”，这就是快慢指针了，可以用快慢指针来解决不少链表中的问题。

准备

编程语言使用Java，实现一个简单的链表结构。

// 链表
class LinkedNode<T> {
    Node<T> head;
    Node<T> tail;

    public Node<T> add(T t) {
        Node<T> node = new Node<>();
        node.value = t;

        if (head == null) {
            head = node;
        } else {
            tail.next = node;
        }
        tail = node;
        return node;
    }
}

// 节点
class Node<T> {
    T value;
    Node<T> next;

    @Override
    public String toString() {
        return value.toString();
    }
}

找到链表的中间节点

给定一个链表和其头节点，找到它的中间节点。

解决思路

常规思路是进行两次遍历，第一次遍历取得链表的长度，第二次遍历找到中间节点。但是使用快慢指针，一次遍历就能实现，只需将快指针步长设为2，慢指针步长设为1，当快指针遍历到链表尾指向null时，慢指针恰好指向链表的中点。其实这种方法不仅可以找到链表的中间节点，找到2/3处，或者3/5处的节点也是同理，快慢指针按比例设置步长即可。

代码实现

public <T> Node<T> getMidNode(LinkedNode<T> linkedNode) {
    Node<T> fast = linkedNode.head;
    Node<T> slow = linkedNode.head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    return slow;
}

找到链表倒数第n个节点

给定一个链表和其头节点，找到它的倒数第n个节点。

解决思路

使用快慢指针，先让快指针跑到第n个节点，慢指针指向头节点，然后以同样的速度向后遍历，当快指针遍历到链表尾指向null时，慢指针恰好指向链表的倒数第n个节点。

代码实现

public static <T> Node<T> getLastN(LinkedNode<T> linkedNode, int n) {
    Node<T> fast = linkedNode.head;
    Node<T> slow = linkedNode.head;
    // 快指针先向前跑n个节点
    for (int i = 0; i < n; i++) {
        fast = fast.next;
    }
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

判断链表中是否有环

给定一个链表和其头节点，判断链表中是否存在环。

解决思路

使用快慢指针，将快指针步长设为2，慢指针步长设为1，从头遍历链表，如果快指针和慢指针相遇，那么链表中则存在环，否则无环。这里可以用赛跑类比：有两个人（A和B）比赛跑步，A跑的比B快，如果是在一条直线跑道上比赛，从同一个起点出发，一直跑下去的话，A与B相距一定越来越远。但是如果将跑道换成环形，一直跑下去的话，A一定会再次与B相遇。

代码实现

public static <T> boolean existRing(LinkedNode<T> linkedNode) {
    Node<T> fast = linkedNode.head;
    Node<T> slow = linkedNode.head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        // 快慢指针相遇，则存在环
        if (fast == slow) {
            return true;
        }
    }
    return false;
}

判断链表中是否有环并找出环的入口

给定一个链表和其头节点，判断链表中是否存在环，如果存在环的话，找出环的入口。

解决思路

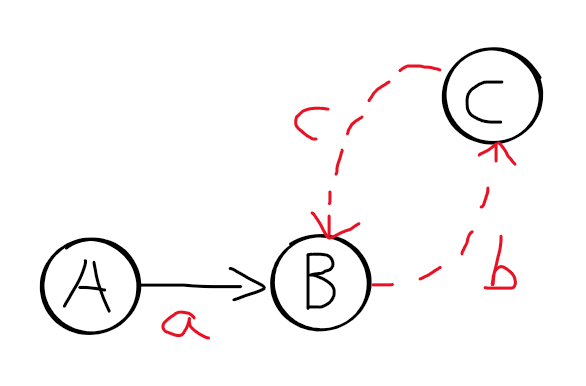
先使用上面的方法判断出链表中是否有环，假设存在环，并且快指针和慢指针在C节点相遇，A->B长度为a，B->C长度为b，C->B长度为c，那么可以得出：2 (a + b) = a + b + n (b + c)，快指针走过的长度为慢指针的两倍，且快指针可能在环中绕了n圈，化简得到：a = n * (b + c) - b，据此分析，可以发现a的长度等于在环中绕n圈再减去b的长度，所以这里可以设置两个指针，一个在A节点，一个在C节点，且以同样的速度前行，两个指针再次相遇的节点即是环的入口。

代码实现

public static <T> Node<T> findEntrance(LinkedNode<T> linkedNode) {
    Node<T> fast = linkedNode.head;
    Node<T> slow = linkedNode.head;
    do {
        // 不存在环
        if (fast == null || fast.next == null) {
            return null;
        }
        fast = fast.next.next;
        slow = slow.next;
    } while (fast != slow);
    // 将慢指针设置为链表头节点
    slow = linkedNode.head;
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

参考：

链表与快慢指针